1.0 Introduction

We currently create the following types of Hexhahedral-Tetrahedral interfaces in I-DEAS:
 

• Linear Hex - Linear Tet           (LHLT)
• Linear Hex - Parabolic Tet      (LHPT)
• Parabolic Tet - Parabolic Tet   (PHPT)

2.0 MPC Schemes

Someone filed an MS8 qapr complaining why MPCs where not getting
created when he meshed linear tets with linear hexes. I initially thought he
was kidding me, later, I realised it is important to put up this "disclaimer"
for the world at large.

NOTE:
The LHLT interface has exact matching nodes and does not need any
new node to be created during tetrahedral meshing. This explains
why this interface does not need MPCs.
 

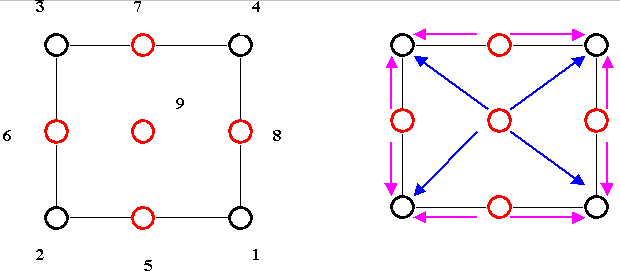
Fig 1. MPCs (blue and pink arrows) tying all 3 DOFs of the Tet nodes (Red) with
           the Hex corner nodes (Black)in a LHPT interface.

Each mid-edge node is tied up to its neighbouring corner nodes, while the mid-face node is tied up to the 4 corner nodes of the hex face. The MPC sets are

Table 1:  MPC Sets for a LHPT Interface

MPC Sets	DOFs	Master Nodes	Slave Node
3	U,VW	1,2	5
3	U,V,W	2,3	6
3	U,V,W	3,4	7
3	U,V,W	4,1	8
3	U,V,W	1,2,3,4	9

For the PHPT interface the only additional node is the ninth node at the element mid-face. This node is tied up to the 4 corner nodes with one set of MPCs and with the 4 mid nodes of the Hex face with another set as shown in Figure 2.

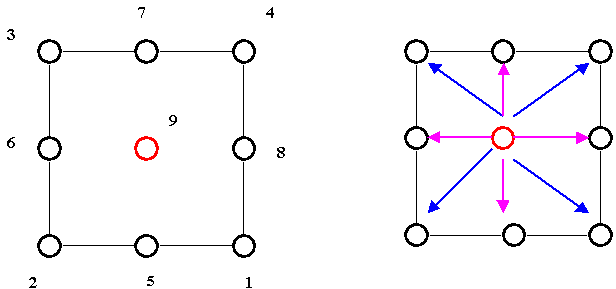
Fig 2. MPCs (blue and pink arrows) tying all 3 DOFs of the Tet mid-face node (Red) with
           the Hex corner nodes (Black) in a PHPT interface.

The MPC sets are listed in Table 2.

Table 2:  MPC Sets for a PHPT Interface

MPC Sets	DOFs	Master Nodes	Slave Node
3	U,VW	1,2,3,4	9
3	U,V,W	5,6,7,8	9

 
 

3.0 MPC Coefficients

The degrees of freedom of a  dependent node can be tied up to n independent nodes using a multi-point constraint in the form

where C₀  is the coefficient of the dependent node and C₁, C₂ , C₃ ...C_n are the coefficients of the independent nodes, A is the constant term. The coefficients normally follow the correlation (especially for the LHPT and PHPT cases)

3.1 LHPT MPCs

For a linear Hex - parabolic Tet interface, 5 additional nodes (4 on the edges and 1 on the mid Hex element face) need to be created to form a 10-noded Tet. Table 1 explains the MPC sets. The coefficients are nothing but the shape functions of the bi-linear isoparametric element as shown in Fig 3. Any 4-sided element in real space can be mapped to a sqaure isoparametric element with coordinates ranging from -1 to 1. In an isoparametric element the same polynomial is used to fit the element to geometry and to the displacement field (hence the coinage "isoparametric").

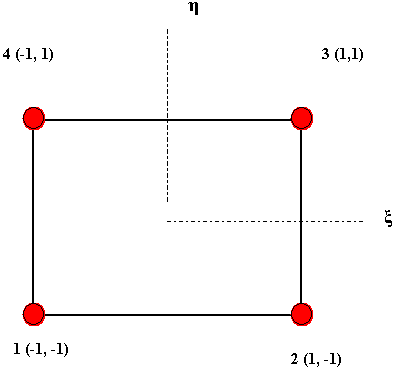
These shape functions of the 4-noded isoparametric element (Fig 3) are given by

  A = 0                                                                                 (4a)

Eqn (4) shows that these shape functions, evaluated for a given zi, eta are actually the mpc coefficients for the LHPT case. The method adopted to determine the MPC coeficients for the mid-face node, goes as

• From the X,Y (of the Hex element face) values of the 9th node determine the zi, eta values
• Substitute the zi,eta values into Eqn (3) to get the coefficients

3.2 PHPT MPCs

Figure 4 depicts an 8-noded bi-quadratic isoparametric element in its natural coordinate system. A Hex20 face can be represented by this element. It's shape functions are given by

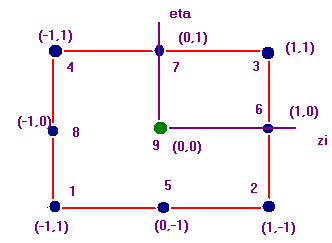
Figure 4. A nine - Noded isoparametric element in its natural coordinate system
 

Eqn 5 lists the mpc coefficients that tie up Node 9 with Nodes 1,2,3,4 (Fig 2). Eqn 6 represents the coefficients for the mid-nodes 5,6,7,8.

If Node 9 is at the centroid of the element in its natural coordinate system, i.e if

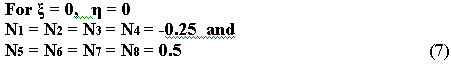
 So the MPC coefficients are C1 = C2 = C3 = C4 = -0.25
                                               C5 = C6 = C7 = C8 = 0.5
 and                                         A = 0;                               (8)

Note: Actually, for the PHPT interface the coefficients, like
the LHPT interface, also depend on the hex-face shape.
But for simplicity they are reduced to that of a rectangular
hex-face.